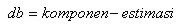Anava Identity : Analisis Varians Sederhana / Satu Jalur (Part II)

Aaah setelah bertapa cukup lama bisa juga akhirnya saya menulis bagian ini. Sebelumnya saya minta maaf pada beberapa teman yang mengharapkan bagian ini segera, karena tidak dapat memenuhi harapan anda semua.
Pada bagian sebelumnya saya sudah membahas mengenai keseluruhan variasi dan satu bagian dari variasi variabel dependen. Nah, bagian berikutnya adalah variasi dari variabel dependen yang tidak mengikuti variasi variabel independennya, sering disebut sebagai variasi error atau variasi residu.
Variasi Error
Beberapa ahli membedakan istilah residu dan error ini. Tapi untuk sementara saya akan menggunakan istilah error saja ya. Variasi error itu adalah bagian yang tidak berwarna dalam gambar di bawah ini (e).

Bagian ini adalah bagian yang tidak mengikuti variasi dari variabel independen. Jika kita melakukan eksperimen, maka bagian ini adalah bagian yang tidak dipengaruhi atau bukan merupakan hasil treatmen dalam eksperimen.Terkadang variasi ini berupa variasi akibat perbedaan individual. Variasi ini akan terlihat dalam tabel data kita, seperti ini:
Bisa kita lihat bahwa meskipun kelompok A1 itu cenderung memiliki nilai yang rendah, tetapi di dalam kelompok A1 tetap ada variasi skornya. Tidak semua menjadi 1 atau 2 atau 3. Jika seluruh variasi variabel dependen mengikuti variasi variabel independen, maka di tiap kelompok hanya akan ada satu nilai untuk semua subjek. Jadi dalam A1 semua subjek akan bernilai 3 misalnya, di A2 akan bernilai 4 semua, dst.Tentu saja ini merupakan peristiwa sangat langka dalam kehidupan sehari-hari. Jadi hampir selalu akan ada variasi dalam tiap kelompok.Oh ya, karena variasi ini terjadi di dalam kelompok, seringkali juga variasi ini disebut sebagai variasi dalam di beberapa buku.

Lalu gimana ngitungnya?
Kita masih bisa menerapkan rumus yang telah diberikan sebelumnya. Hanya saja karena kita menghitung variasi dari tiga kelompok, maka sekarang kita akan menjumlahkan variasi ketiga kelompok ini. Rumus untuk mencari JK di dalam tiap kelompok akan seperti ini:

Nah jika JK dalam dari tiap kelompok ini dijumlahkan akan menjadi seperti ini:

Lagi-lagi bukan maksud saya untuk meminta kamu menghafalkan semua ini. Ini hanya untuk membuktikan bahwa menghitung JK dalam tiap kelompok lalu dijumlahkan itu akan sama dengan menggunakan rumus dalam buku seperti pada persamaan yang terakhir.

Penerapan dalam contoh akan seperti ini:

Nah cobalah menggunakan rumus alternatifnya.

Salah satu keuntungan JK ini adalah sifatnya yang aditif, sehingga kita bisa menjumlahkan JK dalam dan JK antar yang besarnya akan sama dengan JK total. Ini juga merupakan salah satu cara cepat mengecek apakah hitungan kita sudah benar. Benarkah hitungan saya?

Yak betul!. Kemungkinan besar hitungan saya sudah benar. (Cobalah cek lagi. Sebelum ini hitungan saya sempat salah lo. Adakah yang mengetahuinya?).

Apa yang Kita Lakukan Selanjutnya?

Baiklah, sekarang kita sudah punya JK Total, JK Antar, dan JK dalam. Permasalahan dengan JK adalah bahwa semakin besar jumlah subjek yang digunakan untuk menghitung JK, makin besar JKnya. Sehingga meskipun situasinya sama, tapi jumlah N nya berubah, maka JK akan cenderung berubah. Oleh karena itu kita perlu men-standardkan JK ini.

Caranya? Dengan membagi tiap JK dengan derajat kebebasannya. Hmmm rasanya pernah dengar ya. Lagi-lagi derajat kebebasan memiliki rumus umum yang dapat diterapkan di tiap situasi:

Maksudnya komponen di sini adalah komponen yang terlibat dalam perhitungan JK. Jadi misalnya dalam perhitungan JK total, komponen di sini adalah jumlah subjek secara keseluruhan. Estimasi maksudnya berapa banyak statistik yang diestimasi dalam tiap perhitungan. Dalam perhitungan JKtotal kita hanya mengestimasi satu mean populasi, sehingga estimasinya 1. Baiklah rumus lengkapnya begini:

Dalam db Antar, kita menghitung JK dari total tiap kelompok. Oleh karena itu komponen pembentuknya ada sejumlah kelompok, dan kita mengestimasi GrandMean dalam populasi, sehingga hanya ada satu estimasi. Ketika menghitung db dalam, kita menggunakan subjek dalam tiap kelompok sebagai komponennya, dan di tiap kelompok kita mengestimasi satu mean populasi. Oleh karena itu kita mengalikan n-1 dengan banyaknya kelompok. Kemudian dapat dirumuskan juga dengan jumlah keseluruhan subjek dikurangi banyaknya kelompok.

Nah jika kita terapkan dalam contoh akan menjadi seperti ini:
Langkah berikutnya kita membagi JK dengan db yang terkait. JK Total dibagi db Total, JK Antar dibagi db Antar, JK dalam dibagi db dalam. Hanya saja biasanya, dalam tabel anava, hasil bagi JK Total dengan db Total tidak dicantumkan. Lalu hasil baginya berupa apa? Atau apa namanya? Hasil bagi ini dinamai Mean Kuadrat (Mean Square).

Mean Kuadarat? Mana meannya? Kalau diamati sebenarnya jika kita hilangkan semua (-1), kita seolah-olah sedang mencari rerata bukan? begini ilustrasinya:

Bukankah begitu? Oleh karena itu nama dari hasil bagi itu adalah mean dari kuadrat jarak X dari reratanya, yang sering disingkat mean kuadrat. Lalu mengapa dibagi N-1? Ini sangat terkait dengan masalah estimasi. Rerata yang sebenarnya hendak kita gunakan di rumus adalah rerata populasi. Tapi karena kita nggak tahu rerata populasinya, kita mengestimasi rerata populasi ini dengan menggunakan rerata sampel. Karena hanya berupa estimasi maka kita akan selalu kehilangan satu derajat kebebasan. Demikian asal-usulnya.

Kalau kamu amati lagi, sebenarnya Mean Kuadrat ini juga bicara tentang hal lain. Coba amati rumusnya, bukankah familiar? Hmm… yak ok jadi sama dengan suatu rumus ya….. Aha! Rumusnya jadi sama dengan rumus varians! Yup! You’ve got it.Ya, bisa dibilang MK itu setara dengan Varians, menceritakan hal yang sama dengan varians. Jadi kita sekarang kita kembali ke Varians setelah sebelumnya (posting sebelumnya) kita meninggalkannya sementara.

Sekarang mari kita terapkan …(mariii….):

Demikianlah kita temukan MK untuk tiap sumber variasi. Lalu apa berikutnya?

Uji F

Masih ingat gambar berikut ini bukan?

Sebagian dari variasi prestasi siswa itu mengikuti variasi dari model pembelajaran (A), dan sebagian lagi tidak mengikuti model pembelajaran (e). Kalau kita ingin tahu apakah variasi prestasi siswa yang mengikuti model pembelajaran itu besar atau kecil,maka kita perlu membandingkan variasi prestasi yang mengikuti model pembelajaran ini dengan sesuatu. Apakah itu? (kok jadi main tebak-tebakan gini ya?).

Saya mendengar nun jauh di sana menjawab,”dengan variasi error!”, Yak Benar!

Sekarang kita akan membandingkan variasi yang mengikuti model pembelajaran (A), atau bisa dibilang juga sebagai variasi yang di’akibat’kan adanya model pembelajaran yang berbeda, dengan variasi yang tidak mengikuti model pembelajaran (e). Atau bisa disebut juga variasi yang diakibatkan bukan oleh model pembelajaran.

Nah ternyata, jika kita membagi A dengan e kita dapat membandingkannya dengan suatu distribusi khusus dalam statistik yaitu distribusi F. F ini dari nama ‘penemu’nya yaitu Sir Ronald Aymer Fisher. (kenapa nggak distribusi R atau A? ada yang tahu?). Hasil baginya juga diberi simbol F. Jadi :

Nilai F ini kemudian dapat dibandingkan dengan F kritis dalam tabel F atau dihitung dengan computer untuk menemukan p-value nya. Ini seperti yang kita lakukan setelah memperoleh nilai t dari t-test. Sekarang mari kita terapkan lagi dalam contoh:

Dengan F sebesar ini, hampir bisa dipastikan jika p-valuenya pasti lebih kecil dari 0.05. Tapi untuk memastikan kita cek saja. Kamu bisa juga lo menggunakan MS Excel untuk mencari p-value ini. Ketikkan saja perintah berikut ini:

Jika kamu benar mengetiknya maka akan dihasilkan p sebesar 0.002595. Mari kita bandingkan dengan hasil dari SPSS:

Aha! Tepat sama! Wow Keren Banget! Yeah! (jujur saja saya juga nggak nyangka lo angkanya bisa tepat sama seperti ini).

Nah gimana kalo kita ingin melihat tabel F? (hmm….masih ingin lihat tabel F setelah melihat kecanggihan teknologi seperti ini?)

Untuk melihat nilai kritis dalam tabel F kita memerlukan dua nilai db yaitu db Antar dan db dalam untuk mencari nilai kritis dari F.

Nah tugasmu sekarang mencari berapa nilai kritis F untuk tiap taraf signifikasi?

Lalu Apa?

Ketika membandingkan nilai p yang kita dapat dengan taraf signifikasi, kita bisa mengambil kesimpulan mengenai situasi mean di antara kelompok-kelompok. Jika signifikan kita bisa mengambil kesimpulan bahwa perbedaan mean di populasi yang diwakili sampel kita tidak sama dengan nol.

Apakah ini berarti kita dapat mengambil kesimpulan bahwa A1 berbeda dari A2? Atau A2 berbeda dari A3? Atau dapatkah disimpulkan bahwa ketiga kelompok itu saling berbeda meannya?

Jawabnya : TIDAK! (duh galak betul…).

“But why?” (orang sok keminggris nih…).

Because…. Duh ketularan deh. Ini dikarenakan kita menggunakan varians mean antar kelompok bukan menggunakan perbandingan pasangan-pasangan mean. Varians mean antar kelompok akan menjadi cukup besar (untuk menghasilkan F yang signifikan) cukup dengan adanya satu saja pasangan kelompok yang memiliki perbedaan mean yang signifikan. Ilustrasinya begini, misalnya ada mean ketiga kelompok berturut-turut adalah 15, 15, dan 30. Kondisi ini akan membuat varians antar mean tidak sama dengan nol.

Hal ini yang membuat Anova disebut juga sebagai analisis yang bersifat global atau omnibus. Hipotesis nol yang diuji adalah mean kelompok 1 = mean kelompok 2 = mean kelompok 3. Nah ketika hipotesis ini ditolak maka kesimpulannya ada paling tidak satu diantara 3 pasangan kelompok ini yang meannya berbeda. Tapi berapa banyak dan kelompok mana yang berbeda tidak dapat dideteksi oleh Anava. Oleh karena itu dibutuhkan analisis lanjutan untuk melakukannya. Ini disebut juga analisis post hoc atau post hoc test. Post hoc test ini akan dibahas dalam posting tersendiri.

Demikianlah kisah Anava Sederhana ini. Dalam posting berikut-berikutnya saya akan membahas juga mengenai post hoc, anova desain faktorial dan anova untuk amatan ulang (repeated measure).