Nilai-p Dan Istilah-Istilah Terkait (Bagian 1: Nilai p)

Nilai p mungkin merupakan salah satu hasil analisis statistik yang  paling sering dilaporkan baik dalam laporan-laporan penelitian seperti skripsi, tesis dan disertasi atau artikel jurnal ilmiah. Popularitas nilai p ini sepertinya tidak diiringi oleh pemahaman yang benar mengenai makna nilai p dan kesimpulan yang dapat diambil darinya. Kesalahan pemahaman mengenai nilai p ini juga dialami oleh para pengajar statistik dan metode penelitian (baca di sini).  

Tulisan ini hendak memaparkan pemahaman mengenai nilai p dan beberapa istilah yang dekat dengannya. Pembahasan lebih detil mengenai nilai p  dan beberapa misinterpretasinya dapat dibaca dalam tulisan saya yang terbit di Jurnal Manasa dalam tautan sebelumnya. 

Nilai p

Secara ringkas nilai-p merupakan probabilitas memperoleh nilai statistik yang sama dengan atau lebih ekstrim daripada yang diperoleh dari sampel jika hipotesis nul benar. Nilai statistik yang dimaksud dalam kalimat di atas misalnya besarnya perbedaan mean, nilai koefisien korelasi, dll.  Pernyataan "sama dengan atau lebih ekstrim" dapat berarti "sama atau lebih besar", yaitu jika uji statistik ada di 'ekor kanan' (right tail) dari distribusi statistik, misalnya dalam distribusi normal standard ini ini berarti nilai Z positif. Pernyataan tersebut juga dapat berarti "sama atau lebih kecil" jika uji statistik ada di 'ekor kiri' (left tail) dari distribusi statistik (atau Z bernilai negatif dalam distribusi normal standard).

Bagian terakhir dari definisi nilai-p tersebut, "...jika hipotesis nul benar", merupakan bagian yang sangat penting dari definisi tersebut. Ini dikarenakan nilai p selalu dihasilkan dari distribusi statistik dengan 'syarat' atau kondisi hipotesis nul benar. Bagian ini menjadi penting karena dua hal: 

1. Jika distribusi statistik yang diuji tidak sama dengan distribusi statistik ketika hipotesis nul benar, maka nilai-p yang diperoleh dari analisis akan keliru. Misalnya dalam kondisi heteroskedastik, nilai p yang diperoleh menggunakan uji-t (yang tidak dimodifikasi) akan cenderung terlalu kecil karena distribusi yang dihasilkan dari analisis perbedaan mean tersebut sebenarnya tidak mengikuti distribusi t. 
2. Kita tidak dapat menggunakan nilai-p sebagai ukuran probabilitas hipotesis nul benar (berdasarkan data) dan tidak dapat juga menggunakan nilai (1 - p) sebagai ukuran probabilitas hipotesis penelitian kita benar (berdasarkan data). Hal ini dikarenakan nilai p sebenarnya merupakan probabilitas kondisional (conditional probability), dalam hal ini, kondisi yang disyaratkan adalah hipotesis nul benar. Probabilitas kondisional ini dapat diekspresikan sebagai berikut: 

Dalam persamaan tersebut T mewakili nilai statistik yang manapun (bisa korelasi, uji t, dll). ekspresi tersebut juga dapat diringkas 

Sementara probabilitas hipotesis nul benar berdasarkan data penelitian dinyatakan sebagai berikut: 

Dan pernyataan "probabilitas hipotesis penelitian / alternatif benar berdasarkan data " dapat dinyatakan sebagai berikut: 

Kita dapat melihat bahwa ekspresi probabilitas yang ketiga tidak sama dengan ekspresi probabilitas kedua dan keduanya dapat memiliki nilai yang berbeda juga. 

Dengan meminjam Teorema Bayes, kita dapat melihat keterkaitan antara keduanya: 

Teorema tersebut menunjukkan bahwa besarnya probabilitas hipotesis nul benar berdasarkan data penelitian, ditentukan oleh besarnya probabilitas hipotesis nul benar (tanpa pengetahuan mengenai data kita), nilai p dan probabilitas memperoleh data seperti yang kita miliki ketika hipotesis nul salah atau sering disebut sebagai power dari uji statistik. Hubungan antara nilai p dan probabilitas H0 benar berdasarkan data dapat dilihat sebagai berikut: 

Dalam gambar tersebut dapat kita lihat bahwa meskipun hubungan keduanya bersifat monotonik, namun demikian nilai keduanya dapat berbeda. Misalnya ketika analisis memiliki power sebesar 0.3, ketika nilai p sebesar 0.05, maka nilai P(H0 benar | D) mendekati 0.15. Bahkan ketika power sebesar 0.8 sekalipun, besarnya P(H0 benar |D) lebih besar daripada nilai p. Ini artinya besarnya nilai p tidak dapat diinterpretasi sebagai probabilitas H0 benar di populasi berdasarkan data yang kita miliki. 

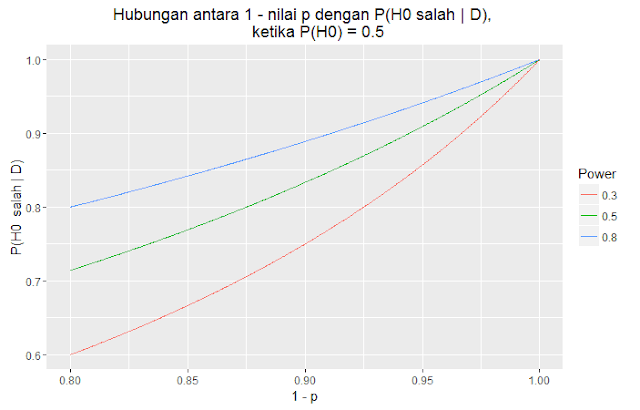
Hubungan antara besarnya (1 - p) dengan probabilitas H0 salah (atau Ha benar) berdasarkan data dapat dilihat dalam gambar berikut: 

Dalam gambar di atas, kita dapat melihat bahwa besarnya nilai (1 - p) cenderung lebih besar daripada probabilitas H0 salah berdasarkan data. Misalnya dengan power dari analisis sebesar 0.3, ketika besarnya (1 - p) = 0.95, probabilitas H0 salah berdasarkan data hanya kurang lebih 0.85, dan menjadi 0.9 ketika analisis memiliki power sebesar 0.5. 

Jadi dapat kita lihat melalui ilustrasi tersebut bahwa nilai p tidak menunjukkan besarnya probabilitas H0 benar berdasarkan data penelitian kita, dan nilai (1 - p) tidak menunjukkan besarnya probabilitas H0 salah berdasarkan data. Nilai p hanya dapat dimaknai sebagai probabilitas memperoleh statistik seperti yang kita temukan dalam data kita atau lebih ekstrim, jika H0 benar di populasi.