t-test (almost) Final Encounter : Asumsi-Asumsi t-test

Seperti yang sudah saya janjikan sebelumnya, saya akan membahas juga asumsi-asumsi dalam t-test. Saya merasa perlu membahas ini tersendiri mengingat cukup banyak kekeliruan yang beredar di sekitar kita mengenai uji asumsi. Saya sendiri tidak berani berkata bahwa pemikiran saya yang saya sajikan di sini paling benar, tapi ini adalah pemahaman saya sampai hari ini, hasil dari baca buku, gosip sana-sini, dengerin kuliah, mimpi, iseng-iseng, dan sebagainya.

Mitos Uji Asumsi

Ada beberapa pemahaman yang menurut saya (saya menekankan sekali ‘menurut saya’ ini karena mungkin menurut yang lain sudah tepat) kurang tepat yang beredar selama ini.

1. Asumsi-asumsi ini adalah asumsi semua teknik statistik parametrik. Yang benar adalah, asumsi-asumsi ini adalah asumsi dari teknik statistik tertentu. Jadi ketika kita membahas t-test, maka asumsi-asumsi ini adalah asumsi dari t-test. Kebetulan saja beberapa asumsi sama antara satu teknik dengan teknik yang lain. (Ini juga merupakan pemahaman saya dulu yang ternyata keliru). Atau beberapa asumsi dari teknik yang berbeda itu sama karena didasarkan pada model yang sama (kita akan membahas ini nanti ketika membahas anava, anareg, dan anakova).

2. Pelanggaran terhadap asumsi yang manapun dapat dipecahkan dengan menggunakan statistik non parametrik. Menurut saya penggunaan statistik non parametrik (distribution free statistics) hanya dapat mengatasi pelanggaran asumsi normalitas saja bukan asumsi yang lainnya. Pelanggaran terhadap asumsi lain (seperti homogenitas varians) hanya dapat diatasi dengan pendekatan yang berbeda dari statistik non parametrik.Pendekatan ini akan dibahas jika nanti kita bertemu dengan tema terkait.

3. Asumsi dari suatu test tidak perlu diuji pemenuhannya oleh data kita. Saya sendiri kurang yakin dengan alasan di balik pendapat ini. Tapi dari yang saya ketahui, pelanggaran asumsi dapat berakibat fatal terhadap kesimpulan yang kita ambil. Bahwa tidak semua asumsi dapat diuji pemenuhannya oleh data kita dengan mudah, itu benar. Beberapa asumsi statistik cukup ribet untuk diuji pemenuhannya oleh data yang tersedia. Beberapa asumsi lain dianggap dapat dipenuhi sejauh teori yang mendasarinya diasumsikan memenuhi asumsi statistik tersebut (bribet banget nggak sih?). Selain itu ada beberapa asumsi yang hampir mustahil untuk dipenuhi dalam penelitian yang sebenarnya, sehingga sejauh kondisi penelitian memuaskan maka asumsi ini dianggap dipenuhi.

4. Pengujian asumsi hanya perlu dilakukan sekali untuk semua analisis yang kita lakukan dalam penelitian. Yang benar adalah bahwa pengujian asumsi harus dilakukan untuk setiap analisis yang berbeda yang kita lakukan dalam suatu penelitian. Analisis yang berbeda di sini maksudnya adalah ketika kita menggunakan teknik yang berbeda atau menggunakan teknik yang sama tetapi menganalisis variabel yang berbeda.

5.Jika uji asumsi gagal maka analisis tidak dapat dilakukan lagi. Ini juga pemahaman yang keliru yang sering membuat jantung para mahasiswa berdegup kencang ketika melakukan uji asumsi. Saya masih ingat teman saya memilih tidak melihat hasil uji asumsi yang dilakukannya selama dua hari untuk menenangkan diri dan mengumpulkan keberanian dulu (true story lho), seakan-akan uji asumsi gagal maka tamatlah riwayatnya. Pelanggaran asumsi jelas dapat membuat ketidaktepatan hasil analisis, tapi tidak selalu berarti analisis tidak dapat digunakan sama sekali. Terkadang hasil analisis masih dapat digunakan dengan beberapa warning atau pemberitahuan akan kelemahan dan keterbatasan. Atau analisis masih dapat dilakukan dengan mengubah bentuk data atau menggunakan pendekatan yang berbeda terhadap data. Terkadang pelanggaran asumsi dapat diabaikan jika kita memiliki alasan kuat mengenai pengabaian yang kita lakukan, atau test yang kita lakukan itu cukup tangguh (robust) mengatasi pelanggaran asumsi.

6. Teknik statistik yang robust berarti dapat mengatasi semua pelanggaran asumsi. Ini sebenarnya masih terkait dengan no 5. Kalo no 5 itu pandangan pesimis, yang ini terlalu optimis. Teknik statistik seperti t dan F memang dapat dibilang robust ketika harus berhadapan dengan beberapa pelanggaran asumsi. Beberapa di sini yang saya tahu hanya asumsi normalitas. Statistik t dan F akan memberikan hasil yang benar-benar keliru (dalam arti tidak dapat ditolerir) jika asumsi homogenitas varian dilanggar. Jadi ke-robust-an t dan F hanya terkait dengan normalitas sebaran data.

Argumentasi saya akan diberikan dalam penjelasan mengenai asumsi t-test ini, beberapa saya tuliskan dalam posting yang berbeda ketika membahas teknik statistik terkait.

Baiklah, jadi apa saja asumsi dari t-test? Beberapa asumsi yang disebutkan di sini berlaku umum, dalam arti asumsi tersebut disyaratkan oleh semua t-test. Beberapa bersifat khusus hanya berlaku untuk t-test tertentu saja. Saya akan memberitahu ketika sampai pada penerapan yang sifatnya khusus.

Pengambilan sampel atau penetapan subjek (random sampling).

Dalam pembahasan di posting sebelumnya, saya beberapa kali menyebutkan “probabilitas jika diambil secara random”. Nilai p yang kita dapatkan dari uji statistik tertentu adalah probabilitas dari munculnya statistik tersebut dalam distribusinya jika pengambilan sampel dilakukan secara random.

Jadi jika pengambilan sampel dilakukan tidak dengan random maka p yang kita dapatkan tidak berlaku lagi. Kita cenderung untuk mendapatkan p yang lebih kecil dari yang seharusnya atau underestimasi nilai p. Hal ini membuat keterwakilan populasi dalam sampel dipertanyakan. Apakah benar hasil yang kita dapatkan dari analisis dapat digeneralisasi ke seluruh populasi? Misalnya ditemukan bahwa siswa putra lebih tinggi hasil tes matematiknya daripada siswa putri, apakah temuan ini dapat digeneralisasi ke seluruh populasi.Ataukah ini hanya kebetulan yang diakibatkan kesalahan pengambilan sampel yang tidak random?

Asumsi ini tentu saja sulit dipenuhi dengan baik dalam hampir semua penelitian (apalagi dengan keterbatasan dana dan tenaga seperti yang dialami mahasiswa...S1 lagi…). Oleh karena itu ada beberapa hal yang dapat dilakukan terkait dengan asumsi ini:

1. Dalam penelitian eksperimen, ketertarikan kita lebih pada efek dari treatment yang kita berikan bukan mean populasi secara keseluruhan. Oleh karena itu, jika kita melakukan random assignment, analisis dan hasilnya masih dapat diinterpretasi dengan baik. Kita masih dapat mengambil kesimpulan yang tepat mengenai efek dari treatment yang kita berikan. Ini diakibatkan random assignment akan menghilangkan bias dalam memasukkan subjek ke dalam kelompok sehingga perbedaan di antara dua kelompok dapat disimpulkan sebagai akibat dari adanya treatment. Yang perlu ditekankan disini adalah ‘ketertarikan lebih pada efek dari treatment’. Maksud saya, sekalipun kita melakukan random assignment, tapi jika tidak melakukan random sampling, kita tidak dapat melakukan generalisasi efek treatment ini ke populasi. Dibutuhkan replikasi-replikasi penelitian pada populasi yang sama untuk memastikan generalisasi dari efek treatmen ini.

2. Dalam penelitian non-eksperimental, kita mengalami masalah yang lebih besar (sejauh yang saya pelajari, teknik statistik memang selalu bermasalah dengan penelitian non-eksperimental … entah kapan akurnya…). Tujuan kita dalam penelitian ini hampir selalu membandingkan dua sampel yang berasal dari dua populasi, dan kemudian hasil dari perbandingan dua sampel itu akan digeneralisasi ke dua populasi. Misalnya kita ingin membandingkan Indeks Prestasi (IP) dari dua kelompok subjek yang berbeda daerah. Jika perbedaan terjadi di sampel dan teruji secara statistik, kita masih tidak dapat mengatakan bahwa perbedaan ini terkait dengan perbedaan asal daerah.Sangat mungkin, meskipun tanpa sengaja, kita mengambil mahasiswa yang ‘pandai’ untuk sampel yang satu dan mahasiswa ‘biasa saja’ untuk sampel lain. Peneliti perlu melakukan beberapa hal terkait dengan isu ini.

(1). Peneliti perlu mengumpulkan informasi sebanyak mungkin mengenai variabel lain dari subjek yang ikut menyumbang terhadap perbedaan IP seperti Inteligensi, asal sekolah, dll. Jadi selain dikumpulkan data mengenai IP, perlu juga dikumpulkan data mengenai Inteligensi tiap mahasiswa.

(2). Peneliti kemudian harus bisa menunjukkan bahwa kedua kelompok tidak memiliki perbedaan dalam semua variabel yang terkait dengan IP. Namun demikian analisis menguji ‘kesamaan’ (sebagai lawan uji perbedaan) antara dua kelompok untuk tiap variabel ini tetap tidak memberikan hasil yang memuaskan karena dilakukan sebagai usaha ‘menerima’ hipotesis nol (dalam pandangan statistik sangat sulit untuk ‘menerima’ suatu hipotesis sebagai benar karena ini mengasumsikan adanya p=1.0. Yang paling memungkinkan adalah ‘gagal menolak’ atau ‘tidak memiliki bukti kuat untuk menolak’ hipotesis nol).

(3). Peneliti dapat juga memasangkan subjek berdasarkan variabel-variabel tersebut, sehingga analisis dilakukan dengan mengasumsikan kedua sampel saling dependen. Dengan demikian analisis akan beralih dari t-test untuk sampel independen menjadi t-test untuk sampel yang dependen (matched paired, paired sample). Atau membuat variabel lain menjadi kovarian lalu mengganti analisis menjadi anakova. Kedua pemecahan ini tetap tidak memberikan hasil memuaskan mengingat kita tidak memiliki seluruh variabel yang menyumbang terhadap variasi IP. Kalaupun kita dapat mengumpulkan seluruh variabel, dibutuhkan sangat banyak subjek untuk dapat membuat analisis berjalan dengan baik.

(4). Semua usaha di atas perlu dan memang sebaiknya dilakukan untuk ‘memperkecil’ kesalahan pengambilan kesimpulan. Namun demikian, seperti yang telah dipaparkan, semua usaha itu tidak dapat menggantikan pengambilan subjek secara random. Oleh karena itu perlu bagi peneliti untuk mencantumkan pelanggaran asumsi ini dan usaha yang telah dilakukan sebagai kelemahan penelitian dan usaha untuk mengatasi kelemahan. Usaha ini saya pandang perlu untuk memberikan informasi yang tepat pada pembaca, tidak terlalu berlebihan (over pede) dan mengurangi kesimpulan yang salah arah, yang seringkali berdampak besar. (masih ingat penelitian mengenai efek mozart? Penelitian ini gagal direplikasi, digeneralisasi secara ngawur pada subjek yang berbeda, tapi banyak dipercaya oleh para praktisi yang kemudian menganjurkannya, menyebabkan terjualnya jutaan kopi dari program, kaset/CD dan bukunya tentu saja dan berdampak pada meningkatnya penghasilan beberapa orang…well ini sisi baiknya sepertinya).

Independensi observasi.

Maksudnya observasi terhadap subjek satu dengan yang lain harus independen satu dengan yang lain. Atau dengan kata lain, hasil observasi dari satu subjek tidak memberikan prediksi apapun mengenai hasil observasi dari subjek lain.

Ada beberapa kasus yang menyebabkan asumsi ini dilanggar antara lain:

1.Jika subjek satu dengan yang lain juga saling mempengaruhi hasil observasi. Contoh subjek menyontek atau memberi contekan subjek lain pada saat pengetesan atau ketika sekelompok orang yang cenderung memberikan respon yang sama seperti orang yang terlibat pertemanan kemudian diwawancarai bersamaan. Respon yang diberikan teman akan dapat mempengaruhi respon yang diberikan seseorang.

2.Jika kita menggunakan lebih dari satu observer, maka sangat mungkin hasil observasi satu subjek dependen terhadap hasil observasi subjek yang lain misalnya jika observer secara tidak sadar membandingkan observasi subjek pertama dengan subjek berikutnya.

3. Jika subjek mengetahui perilaku subjek lain dan kemudian menyesuaikan perilakunya (bisa dalam arti menyamakan atau membuat berbeda). Misalnya jika dalam eksperimen, kelompok kontrol merasa ‘dianaktirikan’ karena tahu bahwa mereka tidak diberi perlakuan khusus, maka mereka cenderung untuk berusaha sekuat tenaga untuk membuktikan bahwa mereka bisa.

4. Jika kita melakukan observasi antar waktu, maka akan ada kemungkinan bahwa perilaku seseorang dalam observasi di suatu waktu mempengaruhi hasil observasi orang yang sama di waktu yang berbeda. Contoh paling konkret adalah jika seseorang diminta mengisi skala dua kali pada dua kesempatan yang berbeda. Jika orang ini masih mengingat respon pada kesempatan pertama, ia mungkin akan memberikan respon yang tidak jauh berbeda pada kesempatan kedua.

Jika observasi satu dengan yang lain tidak independen, maka kita sebenarnya kehilangan lebih banyak derajat kebebasan yaitu sebanyak observasi/subjek yang saling mempengaruhi dalam penelitian. Ini membuat estimasi p dalam sampel menjadi terlalu kecil dibandingkan yang sebenarnya atau kita melakukan underestimasi nilai p.

Selain itu, estimasi standard error akan cenderung lebih kecil daripada yang sebenarnya, sehingga kita akan melakukan overestimasi nilai t yang kita dapatkan.Hal ini akan mengakibatkan underestimasi p, sehingga kita akan cenderung untuk melakukan tipe error I yang lebih besar (misalnya p yang kita temukan 0.05 padahal sebenarnya 0.1).

Distribusi Data Normal

Asumsi ini mungkin asumsi yang paling sering dilakukan oleh peneliti ketika melakukan analisis data statistik menggunakan t-test. Mengapa asumsi ini ada? Mengapa kita perlu memastikan bahwa data kita mengikuti distribusi normal?

Alasan utamanya terletak pada pembuatan tabel t yang dihasilkan dari perhitungan menggunakan populasi yang memiliki distribusi yang normal. Oleh karena itu, jika distribusi populasi penelitian kita tidak normal, bentuk distribusi t yang dihasilkan tidak seperti yang dituliskan dalam tabel pada umumnya. Artinya, jika kita menggunakan tabel pada umumnya untuk mengecek t yang kita dapatkan, kita akan melakukan kesalahan estimasi p. Misalnya seharusnya 0.2, menjadi terlihat seolah 0.05 di tabel.

“Maaf, Pak. Kami pake program komputer untuk analisis statistiknya”. Kalo itu sama saja, karena formula yang digunakan untuk mengestimasi p dalam program analisis statistik juga dihasilkan dari distribusi yang normal. Jadi akan tetap mengalami kesalahan estimasi. Kecuali, jika dengan program komputer kita membuat distribusi t yang baru yang didasarkan pada bentuk distribusi populasi dalam penelitian kita. “Susah?” hehe…banget menurut saya.

Untungnya…ada kabar baik. Ternyata t-test termasuk test yang robust ketika harus berhadapan dengan ketidaknormalan data khususnya jika ketidaknormalan populasi tidak terlalu parah. Melalui beberapa percobaan dapat diketahui bahwa penyimpangan p yang kita dapatkan dari analisis dari p yang sebenarnya tidak terlalu jauh berbeda.

Selain itu dalam central limit theorem disebutkan juga bahwa bagaimanapun bentuk distribusi data di populasinya, semakin besar sampel semakin normal distribusi mean sampelnya (Keppel & Wickens, 2004; Howell, 1984). Dan distribusi terlihat ‘cukup’ normal ketika sampel berisi sekitar 30 orang. Mungkin ini juga alasan mengapa kita sering mendengar ‘minimal sampel’ sebesar 30 orang. Pembahasan mengenai besar sampel akan dilakukan tersendiri.

Jadi aman-aman saja? Tunggu dulu. Ada kasus ketika pelanggaran normalitas bisa berakibat fatal, yaitu jika distribusi data untuk tiap populasi juling (skew) ke arah yang berbeda dan jumlah subjek sedikit dan tidak sama untuk tiap kelompok / sampel. Ini akan membuat error tipe I menjadi asimetris di kedua ujung distribusi (tail). Dalam hal ini, pengujian hipotesis berarah akan mengalami masalah serius dalam arti estimasi p dari tabel akan benar-benar melenceng dari p yang sebenarnya.

Lalu apa yang dapat kita lakukan jika asumsi ini dilanggar? Non parametrik? Hehe sabar ya. Pelanggaran asumsi ini tidak selalu harus diatasi dengan non parametrik tergantung situasi pelanggarannya.

(1).Jika distribusi data kita ternyata multi modal (memiliki beberapa puncak atau beberapa observasi dengan jumlah subjek cukup banyak), maka kita mencurigai adanya subsampel-subsampel. Kita perlu mengidentifikasi subsampel-subsampel ini dan menjadikannya sebagai faktor / variabel baru dalam model. Dengan demikian kita menggunakan teknik analisis lain, yaitu Analisis Varians Dua Jalur.

(2).Jika ketidaknormalan tidak terlalu parah kita dapat meneruskan analisis dengan alasan t-test merupakan uji yang robust terhadap ketidaknormalan.

(3).Kita bisa mentransform data kita menggunakan operasi matematik tertentu tergantung kondisi ketidaknormalan.

(4).Ya apalagi selain menggunakan analisis non-parametrik. Namun perlu diingat, bahwa meskipun analisis non parametrik tidak mensyaratkan bentuk distribusi tertentu, mereka tetap memiliki asumsi yang perlu dipenuhi juga. Ya distribution free statistics tidak sama dengan assumption free statistics (yang setahu saya memang nggak ada statistik yang bebas dari asumsi). Selain itu statistik non parametrik tidak cukup baik digunakan untuk desain yang kompleks (seperti desain dengan dua variabel independen).

Homogenitas Varians antar Kelompok

Homogenitas Varians…selain punya nama lain yang keren, ini memang asumsi yang cukup penting. Pelanggaran terhadap asumsi ini bisa berakibat fatal terhadap kesimpulan yang kita ambil dari analisis statistik. Asumsi ini berlaku khususnya ketika kita berurusan dengan t-test untuk sampel yang independen. Asumsi ini tidak dibutuhkan untuk t-test satu sampel, karena hanya ada satu sampel yang dianalisis. Juga tidak dibutuhkan untuk t-test sampel yang berhubungan, karena varians kelompok antara waktu yang satu dengan berikutnya biasanya homogen.

Nama lain Homogenitas Varians ini adalah Homoscedasticity (baca: homoskedastisiti, cobalah menyebutkan dengan kecepatan normal hehe… bahkan teman-teman kuliah saya yang belajar statistik juga kesulitan menyebutkannya. Homosceblablabla…). Lawan dari homoscedasticity adalah heteroscedasticity. Jika kondisi homoscedasticity terpenuhi dapat dikatakan varians antar kelompok memiliki besar yang sama. Jika varians antar kelompok tidak sama, kita sebut kondisi ini sebagai heteroscedasticity. OK cukup untuk latihan menyebutnya.

Homogenitas Varians di sini tentu saja terkait dengan homogenitas varians di populasi bukan di sampel. Jadi perbedaan varians yang tidak terlalu besar antara kelompok satu dengan yang lain tidak akan berakibat parah. Pelanggaran asumsi ini dapat terjadi atau perlu diwaspadai jika :

(1). Kita membandingkan kelompok berdasarkan gender, status sosial-ekonomi, atau klasifikasi lain. Seringkali terjadi kelompok-kelompok ini secara alami (dari sononya…) memang memiliki perbedaan varians.

(2). Treatmen dalam penelitian eksperimental terkadang juga dapat mempengaruhi variasi skor subjek selain meannya.

(3). Dalam beberapa pengukuran, seperti waktu reaksi, variasi subjek seringkali mengikuti kuantitasnya. Maksudnya dalam kelompok yang memiliki waktu reaksi yang kecil, variasi subjek juga cenderung kecil, sementara pada kelompok dengan waktu reaksi yang besar, variasi subjek juga cenderung besar.

Bagaimana buktiin kalo varians antar kelompok dalam penelitian itu homogen atau tidak? Setelah saya pikir agak lama, sepertinya pembahasan mengenai cara pembuktian ini akan ditulis dalam posting sendiri saja biar lebih detil. Sekaligus cara mencari lewat program SPSS nya.

Lalu apa dampaknya? Beberapa ahli mengatakan bahwa dampak heteroscedasticity ini tidak akan terlalu parah jika kita membandingkan sampel dengan jumlah subjek yang sama. Tetapi dalam penelitian terakhir ditemukan bahwa bahkan dalam sampel dengan jumlah yang sama pun, pelanggaran ini dapat berakibat cukup parah. (Sebagai ilustrasi dapat dilihat dalam Keppel & Wickens, 2004, hal.149).

Ketidakakuratan ini makin diperparah jika besarnya sampel antara kedua kelompok tidak sama, dan juga ketika sampel yang memiliki jumlah subjek terkecil ternyata memiliki varians yang besar. Selain itu pengujian hipotesis berarah juga dapat membuat test makin sensitif terhadap pelanggaran asumsi ini.

Terkait dengan jumlah sampel yang tidak sama, ada prinsip seperti ini:

(1). Jika hubungan antara besar sampel dan varians positif, dalam hal ini sampel yang kecil memiliki variasi yang kecil sementara sampel yang besar memiliki variasi yang besar, maka nilai p yang kita dapatkan dari hasil analisis cenderung lebih besar dari yang sebenarnya. Kondisi ini disebut juga uji statistik kita tergolong konservatif. Dalam hal ini, kesimpulan kita akan memiliki error tipe I yang kecil, tapi cenderung untuk melakukan error tipe II lebih besar.

(2). Jika hubungan antara besar sampel dan varians negatif, yaitu ketika sampel yang kecil memiliki varians yang besar sementara sampel yang besar memiliki varians yang kecil, nilai p yang kita dapatkan cenderung lebih besar dari yang sebenarnya. Jadi jika dari hasil analisis kita dapatkan p=0.05 maka p yang sebenarnya lebih besar (misal p=0.2). Dalam hal ini kita cenderung melakukan error tipe I lebih besar. Jadi ketika kita menyimpulkan hipotesis nol ditolak, sebenarnya hipotesis nol seharusnya tidak ditolak. Kondisi ini disebut juga uji statistik kita tergolong liberal.

Jadi apa yang bisa kita lakukan untuk menghindari kesimpulan yang keliru? Ada beberapa hal yang bisa kita lakukan:

(1). Beberapa ahli menyebutkan jika perbandingan antara varians terbesar dengan terkecil tidak lebih besar dari 4, maka t-test dapat dilakukan tanpa perlu kuatir mengenai heteroscedasticity.

(2). Beberapa ahli lain menyarankan cara yang konservatif (mengurangi tipe error I sekecil mungkin). Cara pertama dengan membagi dua besarnya alpha (tipe error I), atau kita sering menyebutnya taraf signifikasi yang akan kita pakai. Jadi jika kita ingin menggunakan taraf signifikasi 5%, maka sekarang kita mengacu pada taraf signifikasi sebesar 2.5% di tabel.

(3) Cara lain yang konservatif adalah dengan memperkecil db yang kita pakai untuk konsultasi ke tabel. Cara ini ditempuh dengan memilih salah satu sampel dengan n terkecil kemudian mengurangi jumlah subjek dalam sampel ini dengan 1. Jadi dbnya sekarang menjadi n_terkecil-1, bukan (n₁ + n₂ - 2) lagi.

(4) Selain itu kita dapat juga menggunakan db yang dihitung ulang menggunakan formula tertentu untuk meningkatkan akurasi estimasi p. (Saya tidak mencantumkan rumusnya di posting ini, tapi bagi yang berminat dapat mengubungi saya).

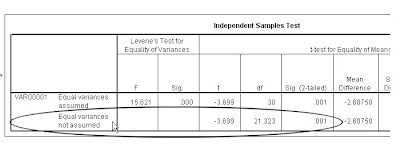
Tapi kita tidak perlu repot menghitungnya, karena selain ribet, juga kita tetap akan kesulitan untuk konsultasi ke tabel karena db yang dihasilkan pasti berbentuk pecahan. Kebayang nggak liat tabel t mencari nilai kritis t untuk db 7.8932? Lalu? Perhitungan ini yang ditampilkan di SPSS di baris equal variances not assumed. Ya, jadi perhitungan di SPSS itu berasal dari rumus ini. (“Bilang kek dari tadi, tiwas deg degan harus itung manual,” sepertinya saya bisa mendengar suara ini). Seperti gambar di bawah ini:

Nah jika di SPSS kita bisa melihat baris ini jika kita meragukan homogenitas varians data kita. Kita bandingkan df (db) di baris atas sebesar 30 dan di bawahnya adalah db yang telah diadjust menjadi 21.323.

(5) Cara kelima ini terkait dengan mengganti analisis dengan analisis yang memungkinkan adanya perbedaan varians di antara kelompok. Kita bisa menggunakan Brown-Forsythe atau James second order method. Kita nggak akan bahas ini banyak di sini ya. Dalam program SPSS hanya ada prosedur Brown-Forsythe atau Welch untuk melakukan analisis yang lain ini.

(6) Cara terakhir untuk berurusan dengan pelanggaran homogenitas varians adalah dengan mentransform data. Ini hanya dilakukan jika kita yakin bahwa hasil transform data tidak akan mengubah esensi data kita (misalnya tidak akan mengubah kondisi berbeda mean menjadi tidak berbeda) atau hasil transform memiliki korelasi yang sangat tinggi dengan data sebelum ditransform.

Demikianlah kiranya pembahasan mengenai asumsi-asumsi dalam t-test. Banyak pemikiran di dalamnya saya ambil dari buku Keppel & Wickens, 2004. Sementara yang lain dari Moore, 2007; Howell, 1986; dan catatan kuliah saya.

Further Readings

Howell, D. C., (1986) Statistical methods for psychology. London: Duxbury Press

Keppel, G. & Wickens, T. D., (2004). Design and analysis, a resercher’s handbook. Fourth edition. Upper Saddle River:Pearson Prentice Hall.

Moore, D. S.(2007) The basic practice of statistics. Fourth edition. New York: W. H. Freeman and Company

t-test Revolution: Paired-Sample t-test

Kita sudah membahas t-test dalam dua posting terdahulu berturut-turut. Posting pertama terkait dengan membandingkan mean sampel dengan mean populasi atau acuan tertentu. Kedua terkait dengan membandingkan mean dari dua sampel yang saling independen. Independen di sini dalam arti keduanya tidak terkait, tidak saling berhubungan, berasal dari dua populasi yang berbeda. Nah sekarang bagaimana jika sampel saling berhubungan atau jika kita melakukan penelitian menggunakan satu sampel tetapi diukur dua kali?

Sampel berhubungan? Ya maksdunya penetapan subjek masuk ke dalam salah satu dari kedua sampel juga dikaitkan dengan variabel lain. Misalnya dalam penelitian mengenai modul pengajaran terbaru, peneliti ingin mengendalikan variabel inteligensi dalam penelitiannya. Oleh karena itu ia mengukur inteligensi dari semua calon partisipannya, kemudian menentukan pasangan-pasangan yang memiliki inteligensi yang sama atau tidak terlalu berbeda. Dari tiap pasangan ini, salah satu akan masuk dalam kelompok yang diberi modul pengajaran terbaru, yang lain diberi modul konvensional. Karena subjek dipasangkan terlebih dulu sebelum dimasukkan dalam kelompok, dapat dikatakan kedua sampel sekarang saling berhubungan.

Contoh Kasus:

Anggaplah penelitian dalam posting kedua dilakukan lagi, tetapi kali ini, karena keterbatasan dana, peneliti hanya dapat mengambil satu sampel saja. Ia berencana untuk melakukan pretest dan posttest dan membandingkan keduanya. Jika hasil dalam posttest lebih tinggi dari pretest, dapat disimpulkan bahwa pelatihan dapat memberikan efek peningkatan motivasi berwiraswasta.

Distribusi Mean Beda Post-Pre

Lagi-lagi kasus ini juga dapat dipandang dengan sudut pandang yang sama dengan membandingkan mean sampel dan mean populasi. Hanya saja kali ini yang dibandingkan adalah mean dari perbedaan post dan pre di sampel dengan mean dari perbedaan post dan pre di populasi. Gambarannya seperti ini:

Mungkin ada yang bertanya,”Maaf, gimana dapetin mean beda post-pre?” Begini, pertama kita mencari terlebih dulu perbedaan antara pre dan post untuk seluruh subjek.

Subjek	pre	post	post-pre (D)
1	6	9	3
2	8	6	-2
	dst

Kemudian perbedaan post-pre dijumlahkan. Apakah tanda negatif dijadikan positif? Jawabannya tidak. Tanda negatif tetap diperlakukan sebagai negatif. Hasil penjumlahan ini kemudian dibagi banyaknya subjek dalam sampel.

Nah, karena yang kita analisis adalah mean dari beda post-pre, maka standard deviasi yang akan digunakan juga adalah standard deviasi dari beda post-pre. Rumus t-test akan terlihat seperti ini:

Beberapa penulis akan menggunakan rumus di sebelah kanan karena terlihat lebih ringkas, dengan D mewakili difference yaitu perbedaan post-pre. Jika kita amati rumus di sebelah kanan, maka kita bisa lihat bahwa rumus tersebut mirip sekali dengan rumus t test untuk membandingkan mean sampel dengan populasi, hanya berbeda simbol saja.

Apakah langkahnya sama? Ya. Setelah kita menemukan perbedaan pre-post untuk tiap subjek, kita bisa memperlakukan data perbedaan pre-post ini seperti kita melakukan t-test satu sampel, hanya saja mean dari beda pre-post di populasi akan sama dengan nol.

Oleh karena itu kita bisa menghitung standard deviasi dari beda pre-post seperti ini:

lalu mengestimasi standard deviasi dari mean beda pre-post.

Derajat Kebebasan

Kalau begitu berapa besarnya derajat kebebasan (db) untuk t-test antar waktu atau sampel yang berhubungan ini? Seperti sudah dijelaskan dalam posting sebelumnya, kita akan kehilangan derajat kebebasan sebanyak parameter yang kita estimasi. Dalam kasus ini hanya ada satu parameter yang kita estimasi yaitu standard deviasi dari beda pre-post di populasi. Estimatornya adalah standard deviasi dari beda pre-post di sampel. Oleh karena itu db dalam t-test sampel yang berhubungan sama dengan:

Kembali ke Contoh Kasus

Lalu bagaimana kita akan menyelesaikan kasus di atas? Anggap saja data yang kita miliki kurang lebih seperti ini:

Subjek	pre	post	Post-pre
1	5	8	3
2	6	9	3
3	4	6	2
4	4	7	3
5	5	7	2
6	6	8	2
7	7	8	1
8	6	7	1

Nah dari data tersebut kita akan menghitung mean dari perbedaan post-pre dan standard deviasi post-pre seperti ini:

Hasil perhitungan tersebut menghasilkan p yang kecil. Oleh karena itu kita dapat berkata bahwa mean dari beda post-pre di populasi tidak sama dengan nol. Dengan demikian kita dapat menyimpulkan bahwa pelatihan memberikan perbedaan antara pre dan post.

Untuk melihat peningkatan, kita tinggal membandingkan saja mean pre dengan post. Jika mean post lebih besar daripada pre maka kita dapat mengatakan ada peningkatan. Atau dengan melihat mean dari beda post-pre. Jika mean tersebut positif maka kita dapat menyimpulkan adanya peningkatan, jika mean tersebut negatif, ini menandakan adanya penurunan.

Dalam kasus ini, mean beda post-pre tersebut positif, sehingga kita dapat menyimpulkan adanya peningkatan motivasi setelah pelatihan.

Alternatif Rumus t-test Sampel yang Berhubungan

Masih ingat dengan rumus t-test hasil penelusuran saya di t-test reloaded? Seperti ini:

Dalam posting tersebut saya menyebutkan bahwa karena kita berasumsi bahwa kedua sampel saling independen maka r_X1X2 akan sama dengan nol. Nah bagaimana jika r_X1X2 tidak sama dengan nol? Jika r_X1X2 tidak sama dengan nol, maka ini adalah kasus t-test sampel yang berhubungan bukan?

Oleh karena itu rumus ini juga dapat digunakan untuk menguji perbedaan mean dua sampel yang berhubungan. Dalam hal ini, X₁ adalah pretest dan X₂ adalah posttest.Tidak percaya? baik mari kita buktikan dengan data kita tadi ya.

Aha! ternyata sama persis (catatan: angka-angka di sini merupakan pembulatan jadi mungkin kamu nggak akan menemukan angkanya persis seperti ini). Jadi memang kedua rumus ini berbicara hal yang sama.

Apakah kamu terpikir sesuatu terkait dengan perbandingan estimasi standard deviasi beda mean dan estimasi standard deviasi mean beda post-pre? Mana yang selalu lebih besar dari yang lain? Pikirkanlah! Diskusikan dengan saya jika kamu menemukan insightnya ya.

t-test Reloaded : Independent sample t-test

Masih ingat posting sebelumnya? t-test the beginning? Kasus yang dimunculkan di sana adalah kasus membandingkan mean sampel dengan mean populasi atau acuan tertentu. Bagaimana jika peneliti ingin membandingkan mean dua sampel?Saya sarankan jika belum membacanya, bacalah dulu karena pemikiran yang ditulis disini merupakan kelanjutan pemikiran dalam posting tersebut.

Contoh Kasus

Mungkin ada baiknya jika kita mulai dengan contoh kasus.Seorang peneliti ingin melihat efektivitas pelatihan kewirausahaan yang dibuatnya. Ia mengajukan pertanyaan penelitian : Apakah pelatihan kewirausahaan yang dibuatnya akan meningkatkan motivasi untuk berwirausaha. Ia memilih secara random sekelompok pemuda dari sebuah desa. Kemudian ia melakukan random assignment untuk menentukan siapa yang akan memperoleh pelatihan terlebih dulu, dan siapa yang diberi pelatihan belakangan. Setelah dua kelompok terbentuk, pelatihan kewirausahaan dilakukan untuk kelompok pertama.

Setelah pelatihan pertama selesai, peneliti melakukan pengukuran motivasi berwirausaha dari kelompok pemuda yang telah diberi pelatihan dan yang belum. Ia berhipotesis bahwa kelompok pemuda yang belum menerima pelatihan akan menunjukkan motivasi yang lebih rendah dibandingkan yang telah memperoleh. Jadi bagaimana caranya melihat perbedaan ini?

Distribusi Beda Mean antara Dua Sampel

Kasus ini dapat dilihat dari sudut pandang yang sama seperti membandingkan mean sampel dari mean populasi: ingin mengetahui berapa besar kemungkinan memperoleh sampel dengan mean sebesar A dari sebuah populasi dengan mean sebesar B, yang dapat dirumuskan begini:

Jika kemungkinan memperoleh sampel dengan mean sebesar A dari populasi dengan mean sebesar B itu kecil, kita dapat bilang bahwa sampel dengan mean A tidak berasal dari populasi dengan mean B.

Dalam kasus ini, yang dibandingkan bukan mean dari satu sampel dengan mean populasi melainkan perbedaan mean dari dua sampel dengan perbedaan mean dari dua populasi, yang dirumuskan sebagai berikut:

Jika kita bandingkan rumusan ini dengan sebelumnya akan terlihat sangat mirip, bukan?

Untuk menemukan besarnya kemungkinan, kita perlu mencari dulu nilai standard dari perbedaan ini. Dalam hal ini kita menggunakan distribusi t. Rumus yang digunakan juga memiliki prinsip yang sama dengan rumus mencari nilai t untuk membandingkan mean sampel dari mean populasi; seperti berikut:

Bandingkan dengan t untuk membandingkan mean sampel dari mean populasi :

Perbedaan keduanya hanya terletak pada apa yang dianalisis. Dalam kasus beda mean yang dianalisis adalah beda mean, sehingga kita menggunakan Standard Deviasi untuk distribusi perbedaan mean. Sementara dalam kasus mean sampel, yang dianalisis adalah mean sampel, sehingga kita menggunakan Standard Deviasi untuk distribusi mean sampel.

Ada satu perbedaan lain antara kedua kasus ini. Dalam kasus membandingkan mean sampel dengan mean populasi, mean populasi bisa memiliki nilai berapapun. Sementara dalam kasus membandingkan perbedaan mean 2 sampel dengan perbedaan mean 2 populasi, kita biasanya menetapkan perbedaan mean 2 populasi sama dengan nol. Jadi dalam hal ini :

Biasanya? Ya, sebenarnya kita dapat menetapkan perbedaan mean 2 populasi bukan nol jika kita memiliki dasar yang kuat untuk melakukannya. Dalam hal ini, yang dimaksud dasar yang kuat adalah teori atau penelitian sebelumnya. Beda mean 2 populasi diasumsikan nol, karena kita ingin menguji apakah pelatihan memberi efek atau tidak. Jika memberikan efek maka beda mean 2 populasi tidak akan sama dengan nol, jika tidak memberikan efek, beda mean 2 populasi akan sama dengan nol (tidak ada perbedaan). Nah kita menggunakan tidak memberikan efek sebagai acuan.

Ya ya saya bisa dengar pertanyaanmu,”mengapa tidak menggunakan ‘memberikan efek’ sebagai acuan?” Alasannya, kita tidak tahu berapa angka yang dapat digunakan untuk menjadi acuan ‘memberikan efek’, dua, sepuluh, lima belas? Sementara “tidak memberi efek” hanya memiliki satu angka yaitu nol. Dalam hal ini jauh lebih mudah menggunakan acuan nol daripada bukan nol.

Standard Deviasi Distribusi Beda Mean

Nah masalah berikutnya terkait dengan bagaimana mengukur standard deviasi distribusi beda mean? Kita akan menggunakan prinsip yang sama dengan distribusi mean sampel, yaitu :

Dengan menggunakan prinsip ini dan juga rumus standard deviasi :kita akan menemukan rumus Standard Deviasi Distribusi Beda Mean sebagai berikut:

Jika ditelusuri terus, persamaan ini akan menjadi seperti ini: (proses penelusuran ini saya cantumkan di akhir posting agar kita tetap fokus ke pembahasan ini)

Karena diasumsikan kedua sampel saling independen satu dengan yang lain maka r_X1X2 akan sama dengan nol. Ini akan membuat persamaan ini menjadi :

Nah persamaan inilah yang sering kita lihat di buku-buku ketika membahas mengenai t-test. Jadi jika kita gabungkan, rumus t-test untuk sampel yang independen akan seperti ini:

Derajat Kebebasan

Hal berikutnya yang perlu kita cari adalah berapa derajat kebebasan (db) untuk t-test sampel yang independen ini. Masih ingat pembahasan mengenai derajat kebebasan t-test untuk satu sampel? Derajat kebebasan terkait dengan berapa banyak parameter yang kita estimasi. Setiap satu parameter kita estimasi, kita akan kehilangan satu derajat kebebasan.

Jika demikian berapa banyak parameter yang kita estimasi dalam t-test ini? Dua? Ya betul! Ada dua, yaitu varians populasi pertama dan kedua. Keduanya kita estimasi menggunakan varians masing-masing sampel (S²_X1 dan S²_X2). Nah, karena kita mengestimasi dua parameter, kita akan kehilangan 2 derajat kebebasan, satu untuk tiap sampel. Oleh karena itu db dari t-test sampel yang independen dapat dirumuskan seperti ini:

Kembali ke Contoh

Baiklah, kita kembali ke contoh untuk melihat aplikasi t-test ini. Anggap saja kita mendapatkan perhitungan berikut dari data.

	X1 (pelatihan)	X2 (belum)
Mean	89	67
Varians	25	36
n	10	10

Dari data seperti ini dapatkah kita mengatakan bahwa kelompok pemuda yang telah memperoleh pelatihan itu memiliki tingkat motivasi yang lebih tinggi daripada yang belum memperoleh pelatihan? Mari kita terapkan data ke dalam rumus :

Hasil perhitungan menunjukkan bahwa kesempatan untuk mendapatkan perbedaan sebesar itu dari dua populasi yang perbedaannya nol adalah 0.000. Nilai p sebesar ini dianggap sangat kecil, sehingga kita dapat berkata ada perbedaan yang signifikan antara mean kedua kelompok. Ini berarti perbedaan yang terjadi di antara kedua sampel dapat mencerminkan perbedaan di populasinya.

Alternatif Rumus t-test

Selain rumus yang telah disajikan sebelumnya, t-test juga bisa menggunakan rumus lain, seperti berikut:

Ide ini berasal dari pemikiran bahwa varian dari kedua sampel dapat dicari reratanya. Rata-rata dari varians kedua sampel ini yang disebut S² pooled. Rumus ini hanya berlaku jika varians kedua sampel tidak jauh berbeda. Jika varians kedua sampel jauh berbeda maka rumus ini akan memberikan estimasi yang keliru. Hal ini akan dibahas dalam posting mengenai Asumsi dalam t-test.

Nah demikianlah t-test untuk sampel yang independen berasal. Dan juga bagaimana aplikasinya. Kita masih ada dua pembahasan lagi nih untuk posting berikutnya: mengenai t-test untuk sampel yang berhubungan atau antar waktu, dan asumsi dalam t-test.Besar harapan saya, pembaca bisa menemukan benang merah (atau warna apapun boleh) antara Z, t-test satu sampel dan t-test sampel independen ini.

Penelusuran Rumus Standard Deviasi Beda Mean

Seperti yang saya tulis sebelumnya saya mencantumkan ini di akhir posting agar tidak ‘mengganggu pemandangan’, khususnya bagi yang agak mengalami alergi dengan rumus matematika. Penelusuran ini saya tampilkan untuk ‘pembuktian’ mengenai pemikiran saya tentang kesamaan pemikiran Z, t-test satu sampel, dan t-test sampel independen (dan nanti t-test sampel yang dependen atau antar waktu).

Penulusuran ini berjalan seperti ini (Peringatan saya, memandang pembuktian rumus sekecil ini dapat merusak mata. Oleh karena itu silahkan diklik saja supaya ditampilkan dalam image yang lebih besar) :

t-test : The Beginning

Setelah lelah bercerpen ria. Sekarang saya mau istirahat dulu dari menulis cerpen, dan menyajikan materi seperti biasa yang saya sukai, bertutur. Kali ini saya ingin menunjukkan keterkaitan antara Z score dengan Uji-t yang manapun. Dengan melakukan ini saya berharap kita tidak lagi harus menghafal rumus mati-matian atau bolak-balik catetan kalo ujian. Dengan pemahaman ini, saya berharap kita cukup mengingat satu rumus saja dan prinsip dasar serta logikanya sehingga ketika berhadapan dengan tiap situasi, kita bisa menerapkan variasi dari rumus tersebut.

Z score
Sebenarnya ide awal pengujian statistik khususnya t-test berasal dari Z-score… Ya, ya saya bisa dengar suara di ujung sana bertanya,”Ehm ehm maaf, Pak, Z-score itu apa ya?”. Tenang saja, itu makanya saya kasih judul sub bab ini seperti itu karena ini yang mau saya bahas pertama kali (ribet banget nggak sih ngomongnya?).

Z-score adalah skor standard berupa jarak skor seseorang dari mean kelompoknya dalam satuan Standard Deviasi. Z-score memiliki banyak sekali kegunaan, misalnya membandingkan posisi seseorang dengan orang lain dalam kelompok masing-masing. Budi, mendapat nilai 7 sementara Andi 9. Budi berargumen bahwa guru kelasnya itu pelit nilai sementara guru kelas Andi itu baik hati. Nah untuk membuktikan apakah memang Budi mendapat nilai yang sama atau lebih baik dari Andi, kita menggunakan Z-score. Pemikirannya begini, karena semua anak di kelas Andi atau Budi mendapat perlakuan yang sama (tentu saja dengan asumsi tidak ada anak emas, anak perak, dll), kita tinggal membandingkan posisi Budi dan Andi dalam kelas mereka masing-masing. Jika posisi Budi lebih tinggi daripada Andi dalam kelas mereka, kita bisa bilang Budi sebenarnya memiliki nilai lebih baik dari Andi.

Rumus? Mari kita baca definisi Z-score sekali lagi: jarak skor seseorang dari mean kelompoknya ini berarti:

dalam satuan Standard Deviasi, ini berarti jarak tadi dibagi Standard Deviasi. Rumusnya jadi begini:



Kegunaan lain dari Z-score adalah kita bisa menghitung persentase orang-orang yang berada di atas atau di bawah skor tertentu. Nah, biasanya diasumsikan sebaran data yang diacu itu normal. Lagi-lagi saya mendengar suara nun jauh di,”Mengapa?”. Karena bentuk ini yang paling mudah dijadikan acuan. Sebenarnya bentuk lain juga bisa dihitung persentasenya, hanya saja akan sangat banyak variasinya sehingga kita harus menghitung kasus per kasus. Ini akan menyulitkan pembuatan formula yang dapat berlaku umum. Oleh karena itu sebaran data yang normal ini yang dijadikan acuan.

Gambarannya seperti ini:

Dalam gambar ini bisa dikatakan area berwarna biru adalah persentase banyaknya orang-orang yang skornya lebih besar dari -2 SD. Sementara area yang berwarna hijau menggambarkan persentase orang-orang yang skornya lebih kecil dari -2SD atau bisa dibilang juga lebih ekstrim. Nah untuk mendapat angka persisnya bisa kita lihat di tabel. Caranya? Lihat posting sebelumnya mengenai Confidential Interval ya.

Contoh? Oke oke… Misalnya contoh yang kita lihat tadi. Benarkah Andi memiliki kemampuan lebih dibanding Budi? Kita tahu bahwa skor Andi itu 9 sementara Budi itu 7. Nah misalnya saja di kelas Andi rata-rata murid mendapat skor 8, sementara Budi 5. Standard Deviasi di kelas Andi dan Budi misalnya sama-sama 1. Dan kita anggap saja kedua kelas memiliki sebaran data yang normal. Nah mari kita terapkan data ini:

OK, dari perhitungan terlihat bahwa ternyata Andi hanya berada dalam jarak 1 SD dari mean kelompoknya, sementara Budi 2 SD lebih tinggi dari mean kelompok. Dari sini sudah terlihat bahwa Budi sebenarnya memiliki skor yang lebih tinggi. Ini makin terlihat jika kita membandingkan persentase orang-orang yang berada di bawah skor mereka. Andi berada di atas 84.13% murid-murid lain di kelasnya, sementara 97.72% murid-murid di kelas Budi berada di bawah nilai Budi. Ini berarti Budi termasuk murid pintar di kelasnya, karena hanya ada 2.28% (100%-97.72%) murid di kelas Budi yang memperoleh nilai sama seperti Budi atau lebih tinggi.

Kita juga bisa berkata bahwa Budi dan 2.28% murid di kelasnya termasuk murid langka, jarang atau sulit ditemui (kayak pejabat aja ya sulit ditemui). Dengan kata lain, jika kita masuk ke kelas dan memilih secara random, kecil kemungkinan kita akan memilih Budi dan 2.28% temannya. Ini yang kemudian akan jadi dasar penentuan uji hipotesis menggunakan signifikasi.

Central Limit Theorem

Nah ide ini kemudian juga digunakan untuk mencari berapa besar probabilitas kita memilih secara random sebuah kelompok dengan mean tertentu dari populasi dengan mean tertentu. Duh bingungin ya. Misalnya begini: berapa besar probabilitas memperoleh sekelompok mahasiswa dengan rata-rata IP di atas 3.5 dari populasi mahasiswa yang rata-rata IP-nya 2.5 secara random?

Jika kita menganggap rerata sampel sebagai unit analisis seperti Budi dalam kasus di atas, kita bisa menerapkan ide yang sama dengan Z score tadi, lihat gambar berikut:

Lingkaran besar ini menggambarkan kelas Budi dalam kasus di atas. Lingkaran kecil di dalamnya menggambarkan tiap siswa di kelas tersebut termasuk Budi. Anggap saja lingkaran kecil tersebut banyak.

Dalam kasus tersebut Budi dan siswa di kelasnya menjadi unit analisis. Tiap siswa merupakan satu unit analisis. Jika kelas Budi berisi 40 siswa, maka ada 40 unit analisis atau kita sering menyebut dengan n = 40. Kita menghitung mean kelas, SD kelas dari unit-unit analisis ini.

Sekarang kita bandingkan seandainya sampel yang menjadi unit analisisnya.

Nah dalam kasus mahasiswa gambarnya kurang lebih seperti ini. Sama? Ya tentu saja karena saya hanya copy paste hehe… Tapi memang idenya sama. Sekarang, lingkaran besar merupakan populasi, dan lingkaran kecil adalah sampel mahasiswa termasuk sampel yang memiliki rerata 3.5.

Jika kita ingin tahu berapa persen sampel mahasiswa yang reratanya 3.5, kita dapat menggunakan ide yang sama dengan kasus Budi tadi. Benarkah? Baiklah kita coba terapkan rumus Z di atas.

Hm…sepertinya ada yang salah? Ya berapa SD-nya saudara-saudara? Perhitungan di sini sebenarnya sama dengan perhitungan SD dalam kasus Budi. Perbedaannya, dalam kasus Budi kita menghitung SD dari distribusi skor individu, sementara dalam kasus ini kita menghitung SD dari distribusi mean sampel atau mean dari sekelompok individu. Lihat ilustrasi berikut:
Rumusnya? Plêk padha (persis sama dalam bahasa Tegal). Lihat perbandingan berikut ini:

Sama kan?
Hanya saja masalahnya, kita bisa menarik sampel hingga jumlah yang tak terbatas berkali-kali (k=tak terhingga), sehingga menghitung SD dari distribusi mean sampel hampir merupakan pekerjaan mustahil buat kita. Selain itu cara ini mengharuskan kita mengambil sampel sangat banyak dan menghitung meannya padahal ketertarikan kita hanya pada satu sampel dengan mean 3.5. Ini tentunya tidak efisien alias repot!

Untung saja ada Central Limit Theorem (CLT). Salah satu hal yang dinyatakan oleh CLT ini adalah SD dari distribusi mean sampel besarnya akan sama dengan hasil bagi antara SD populasi dengan akar dari besarnya sampel, atau begini:

Yang perlu diingat di sini, s_X adalah SD dari populasi bukan SD dari sampel yang kita dapatkan. Tentu saja ini akan menimbulkan masalah baru, tapi untuk sementara anggap saja kita tahu besarnya SD dari populasi.

Jadi mari kita bereskan masalah tadi. Misalnya kita tahu bahwa besarnya sampel mahasiswa dengan rerata IP 3.5 yang kita miliki adalah 9 orang dan SD dari populasi adalah 1.8 Berapa persentase mendapatkan sampel dengan mean IP 3.5 atau lebih besar?

Ini berarti kemungkinan kita memperoleh sampel dengan mean sebesar 3.5 dalam populasi ini sebesar 4.78%. Besarkah atau kecilkah kemungkinannya? Itu tergantung penilaian masing-masing. Beberapa orang menggunakan patokan p lebih kecil dari 0.05 sementara yang lain menggunakan judgment, penilaian sendiri (thanks for Dr Huberty). Penilaian sendiri ini tentunya terkait dengan pertimbangan-pertimbangan tertentu seperti apakah ini penelitian awal atau lanjutan, temuan-temuan dalam penelitian sebelumnya, dsb.

Jadi aplikasinya begini: jika kita mengambil suatu sampel (sebesar 9 orang) secara random dari suatu populasi A, kemudian menghitung mean IP-nya dan mendapatkan angka 3.5, dapat kita simpulkan bahwa sampel kita ini kecil kemungkinannya (jika 4.78% dianggap kecil) berasal dari populasi dengan mean IP 2.5. Kemudian disimpulkan bahwa sampel ini bukan berasal dari populasi dengan IP 2.5. Ini yang kemudian diberi label signifikan: ada perbedaan signifikan antara mean populasi dengan mean sampel. Kesimpulan lanjutannya jadi seperti ini: karena sampel kita kecil kemungkinannya berasal dari populasi dengan mean IP 2.5, ini berarti populasi A (tempat sampel kita berasal) kecil kemungkinannya memiliki mean IP sebesar 2.5.

OK deh. Beres.

Ya ya ya saya tahu. Tadi saya bilang kalo menggunakan standard deviasi populasi (s_X) akan menimbulkan masalah tersendiri. Masalahnya, kita seringkali (bahkan hampir selalu) nggak pernah tahu berapa besarnya standard deviasi di populasi. (Saya seakan bisa mendengar,”Hah?! Lalu?”) Ya ya saya bisa paham perasaanmu, seperti tertipu begitu? Tenang, penjelasan tadi memang perlu untuk memahami apa yang akan saya bahas berikutnya dan juga melihat kaitan keduanya.

Distribusi t

Karena kita nggak pernah bisa tahu standard deviasi populasi, kita perlu melakukan estimasi terhadap standard deviasi populasi ini. Estimasinya berasal dari… Yak betul! Dari standard deviasi sampelnya. Jadi kita akan mengganti s_X dengan SD_X. Di sini muncul masalah baru (duuh masalah mlulu kapan selesainya?). Ternyata dengan mengganti s_X dengan SD_X distribusi sebaran mean sampel jadi berubah. Bukan lagi mengikuti kurve normal, tetapi mengikuti distribusi baru. Aha! Tepat sekali! Distribusi baru ini adalah distribusi t (t kecil).

Distribusi ini ditemukan oleh seseorang bernama William Gosset dengan nama samaran ‘student’. Oleh karena itu statistik ini disebut ‘student t distribution’. Dia adalah salah satu staf di perkebunan anggur milik Guiness. Hmm… Siapa bilang statistik itu membosankan. Probabilitas ditemukan di meja judi, distribusi t ditemukan di tempat pembuatan bir, F test (yang akan kita pelajari berikutnya) berasal dari jamuan minum teh. Adakah yang lebih menyenangkan dari ini? (Thanks Jon, for the illustration).

Nah sekarang rumusnya akan berubah sedikit menjadi seperti ini:
Ya kita akan menggunakan istilah estimated karena standard deviasi dari distribusi mean sampel ini adalah hasil estimasi dari sampelnya.

ini sering juga disebut estimated standard error atau banyak yang menyebut hanya sebagai standard error. (Saya bisa mendengar beberapa berteriak,”Aha!” memperoleh pencerahan).

Teknik atau rumus ini kemudian disebut sebagai one sample-t test, atau t-test untuk satu sample, digunakan untuk menguji perbedaan antara mean satu sample dengan mean populasi atau suatu acuan lainnya.

Dengan demikian sekarang jadi jelas bukan kaitan antara Z dan t. Semua prosesnya kemudian menjadi sama dengan jika kita menggunakan Z. Perbedaannya terletak pada tabel acuan distribusinya. Jika menggunakan Z kita mengacu ke tabel distribusi normal, di sini kita akan menggunakan acuan tabel distribusi t. Selain itu distribusi t ternyata juga berbeda-beda untuk tiap derajat kebebasan/degrees of freedom (db / df). Jadi untuk tiap db akan ada distribusi t-nya sendiri sehingga sangat penting untuk mengetahui db ini. Makin besar dbnya, distribusi t ini akan menyerupai distribusi normal.

Derajat keBebasan?

Ya derajat kebebasan (db). Db ini bersumber dari pemikiran ini: tiap kali kita mengestimasi parameter (karakteristik populasi), kita akan kehilangan satu derajat kebebasan. Ilustrasinya begini: misalnya ada populasi dengan mean sebesar 10. Jika kita diijinkan untuk mengambil sampel sebesar 10 orang dari populasi ini, berapa banyak orang yang dapat kita ambil dengan bebas? Misalnya kita ambil orang pertama secara bebas, ia memiliki skor 14. Orang kedua masih dengan bebas, ia memiliki skor 8. Kemudian berturut-turut orang selanjutnya: 15, 6, 11, 14, 8, 6, 5 dan orang kesepuluh…. Tidak. Orang kesepuluh tidak dapat diambil secara bebas lagi. Jika sudah ada 9 angka, angka ke sepuluh tidak lagi dapat ditentukan dengan bebas agar mendapat estimasi yang sama (mean = 10). Misalnya jumlah skor-skor tadi adalah 87. Agar estimasi yang kita dapatkan sama, yaitu mean = 10, orang kesepuluh harus ditentukan sebesar 13. Dengan demikian dapat dikatakan kita kehilangan satu derajat kebebasan.Nah db inilah yang kemudian digunakan untuk melihat tabel t.

Dalam perhitungan kita tadi, kita hanya mengestimasi satu parameter yaitu s_X, oleh karena itu kita hanya kehilangan satu derajat kebebasan, sehingga db yang kita miliki sekarang adalah N-1, yaitu 49-1 = 48.

Contoh

OK, contohnya begini. seorang peneliti sosial ingin mengetahui apakah desa A itu dapat digolongkan dalam desa miskin atau tidak. Peneliti kemudian mengambil data penghasilan penduduk dari sampel yang diambilnya secara random sejumlah 49 KK. Peneliti kemudian menghitung standard deviasi dan mean dari penghasilan 49 KK ini, ditemukan S_X=140000, dan Mean penghasilan= 290000 rupiah perbulan. Misalnya batas kemiskinan itu adalah 250.000 rupiah perbulan. Jadi apakah desa A masih dapat digolongkan sebagai desa miskin? Mari kita buktikan:

Dari perhitungan di atas kita mendapatkan p(t(48))=2.55% (baca: probabilitas munculnya t dengan df=48 sama atau lebih besar dari 2 adalah 2.55%). Karena angka sebesar 2.55% itu termasuk kecil (menurut saya) saya bisa berkata bahwa desa A sudah tidak dapat dianggap sebagai desa miskin lagi, tapi sudah di atas peringkat desa miskin. Berapa peringkat di atasnya? Itu tidak dapat dijawab dalam penelitian lagi, diperlukan penelitian lagi dengan acuan yang berbeda.

Nah sekarang baru beres? Belum. Pertanyaan selanjutnya: bagaimana jika yang saya inginkan adalah membandingkan mean dari dua sampel, mean tiga sampel, mean dari sampel-sampel yang berkaitan? Jika demikian tunggu posting berikutnya ya.